メディアチームトライ木をビットスライスとパトリシア木でコンパクトにしてみた！
メディアチームIT技術
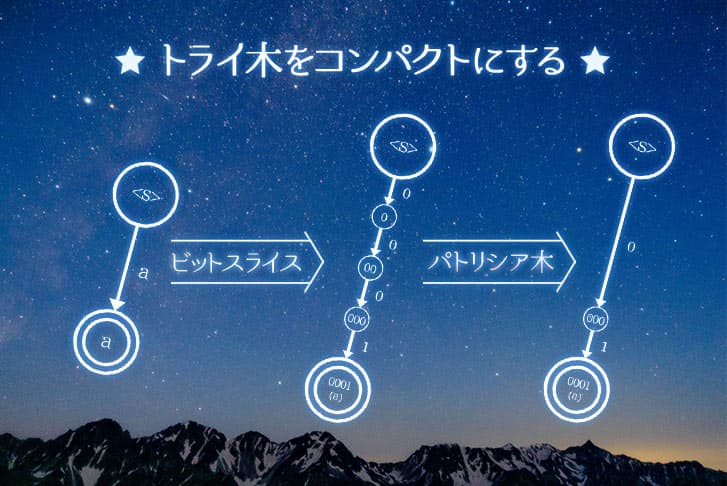
「ビットスライス」「パトリシア木」を用いて、トライ木の問題点を解決したい！
前回の記事では、トライ木というデータ構造を紹介し、トライ木を用いた辞書の実装を行いました。
トライ木は、非常に高速で文字列を検索できる優れたデータ構造ですが、問題点もあります。
本記事では、まず、トライ木の問題点について説明します。
その後、その解決方法である「ビットスライス」「パトリシア木」を用いて、前回と同様の辞書システムを実装します。
前回の記事
2019.08.08トライ木で高速な辞書を作ってみた！トライ木で高速な辞書を作りたい！トライ木（英: trie）というデータ構造を知ってますか？トライ木はテキストを扱う際に...
このトライ木の問題点
前回の記事で実装したトライ木には、サイズが大きくなりやすいという問題点があります。
前回の実装にて、トライ木の1つのノードは、以下のように定義されていました。
1class TrieNode:
2"""
3Trie木の1ノードを表すクラス
4
5Attributes
6----------
7item : str
8登録された単語の読み方
9単語終端ノード以外の場合はNone
10
11children : list
12子ノードのリスト
13"""このうち、問題となるのは、子ノードのリストであるchildren です。
前回の実装では、children はアルファベット数分のサイズを持つリスト(配列)として保持されていました。
これにより、トライ木全体のサイズは少なくとも「ノード数 × アルファベット数」となります。
前回は、ascii文字のみの対応だったため、アルファベット数は「128」でした。
しかし…例えば日本語に対応しようとした場合、「ひらがな」「カタカナ」「漢字」と、アルファベット数は「数千」、あるいは「数万」にもなります。
これは、とてもメモリ上に保持できるサイズではありません。
そこで今回は、このトライ木のサイズを削減するためにビットスライスという手法と、パトリシア木という木構造を紹介します。
ビットスライス
まずは１つ目の手法である、ビットスライスを紹介します。
この手法は、トライ木のサイズ(ノード数 × アルファベット数)のうち、アルファベット数を少なくするための手法です。
コンピュータ上では、「a」や「b」といった文字は、ビット列として表現されています。
そこで、「a」や「b」といった文字をビット列に分解し、分解されたビットを文字の代わりにアルファベットとして用いることで、アルファベット数を少なくすることができます。
1ビットで表現できるのは「0」と「1」ですから、この手法によりアルファベット数は「2」となります。
上の図は、「a」という単語が格納されたトライ木をビットスライスにするものです。
上の図において、左のシンプルなトライ木を、「a」が「0001」というビット列で表されると仮定して、ビットスライスしています。
ビットスライスの問題点
アルファベット数を大幅に減らすことができるビットスライスですが、この手法にも問題点があります。
先程の図を見た時点でお気づきの方もいらっしゃるかと思いますが、ビットスライスを用いるとアルファベット数が減るかわりにノード数が増えます。
本来1文字である「a」という文字をビット列で表すと、(4ビットで表されていた場合)「0001」という様に4文字分になります。
これにより、アルファベット数は「2」になりますが、ノード数は4倍になってしまいます。
このノード数が増加してしまうという問題を解決するために、パトリシア木というデータ構造を用います。
パトリシア木
パトリシア木は、Trie木のノード数を削減できるデータ構造です。
トライ木では、1つのノードには1つのアルファベットが対応していました。
しかし、パトリシア木では下の図のように分岐がないノードを省略し、1つのノードに複数のアルファベットを対応させることでノード数を削減しています。
パトリシア木の実装(準備)
それでは、実際にパトリシア木を実装し、辞書システムを作っていきます。
言語は、「Python（パイソン）」を用います。
要件
トライ木の記事のときの要件に、サイズに関する要件が加わりました。
- 単語とその読み方のペアを登録する
- 単語を入力することで読み方を出力する
- 単語に使える文字はasciiのみ
- ビットスライス、パトリシア木を用い、できるだけサイズを小さくする
単語とその読み方のペアとして、今回も前回同様以下のデータを用います。
1単語:読み方
2a:エー
3ab:エービー
4ac:エーシー
5abc:エービーシー
6bc:ビーシーでは、準備段階としてパトリシア木の実装に用いる構造体から作っていきましょう。
- パトリシア木のノードを表すPatriciaNodeクラス
- パトリシア木の実体を表すPatriciaクラス
今回は、パトリシア木のノードを表すPatriciaNodeクラスと、パトリシア木の実体を表すPatriciaクラスを用います。
PatriciaNodeクラス
まずは、PatriciaNodeクラスについて紹介していきます。
PatriciaNodeクラスは、3つの変数を持ちます。
item
item は、辞書引きを行った際にとってきたい情報です。
今回は、読み方を引いてくる辞書なので、itemには登録する単語の読み方が入ります。
children
children は、どの文字でどのノードに遷移するかを表したリストです。
今回は、アルファベット数（VOCAV_SIZE）が2なので大きさは2となります。
sub_str
sub_str は、トライ木では必要なかった新たな変数です。
パトリシア木では、1つのノードに複数のアルファベット(ビットスライスの場合はビットとなる)が対応するため、何ビット目をチェックすれば良いのか分からなくなってしまいます。
そこで、sub_str として対応するアルファベットを保持しておくことで、どのビットを比較すれば良いかが分かるようにします。
1VOCAB_SIZE = 2 # アルファベット数
2
3class PatriciaNode:
4 """
5 Patricia木の1ノードを表すクラス
6
7 Attributes
8 ----------
9 item : str
10 登録された単語の読み方
11 単語終端ノード以外の場合はNone
12
13 children : list
14 子ノードのリスト
15
16 sub_str : str
17 そのノードに対応する部分文字列
18
19 """
20
21 def __init__(self, item = None, sub_str = ""):
22 self.item = item
23 self.children = [-1 for i in range(VOCAB_SIZE)]
24 self.sub_str = sub_strPatriciaクラス
続いて、Patriciaクラスの説明を行います。
Patriciaクラスは、パトリシア木の実体を表すクラスで、nodes という変数を持ちます。
nodes
nodes は、PatriciaNodeのリストとなります。
1class Patricia:
2 """
3 Patricia木を表すクラス
4
5 Attributes
6 ----------
7 nodes : PatriciaNode
8 ノードのリスト
9 """
10
11 def __init__(self):
12 root = PatriciaNode()
13 self.nodes = [root]パトリシア木実装(補助メソッド)
それでは、パトリシア木の中身を実装していきます。
が、先に「挿入」「検索」どちらの処理でも共通して使う__search_longest_match() というメソッドの解説を行います。
__search_longest_match() についての解説
- __search_longest_match() は、Patriciaクラスのクラスメソッド
このメソッドは、検索文字列をビット列に変換したものを入力として、パトリシア木の探索を行います。
前編で説明したとおりパトリシア木では、1つのノードが複数のアルファベットに対応しています。
そのため、あるノードまで遷移してきた場合でも、検索文字列がそのノードに対応するアルファベット列の全てと一致するとは限りません。
そこで、__search_longest_match() では、入力文字列をもちいて、一致する最後のノード（node_index）まで探索を行い、そのノードのアルファベット列のどこまで一致したのかを表すmatch_str と、また、一致しなかった部分を表すrest_str を返します。
上の図は、「a」「b」「abc」という3単語を格納したパトリシア木において、ab（0001 0000）を検索したときのそれぞれの変数の値です。
この場合、id=4 のノードまで遷移してきているので、node_index は 4 となります。
また、id=4 のノードの中でも、「0000」というビット列までは一致しており、「1011」は一致していないので、match_str は 0000、rest_str は 1011 となります。
__search_longest_match() の実装を単純にするために、2つの文字列が先頭から何文字目まで一致しているかを調べる__match() メソッドも作成しています。
コード
1class Patricia:
2 def __match(self, word_b1, word_b2):
3 """
4 word_1がword_2に先頭から何文字目まで一致しているかを調べる
5
6 Parameters
7 ----------
8 word_1 : str
9 比較対象ビット列
10
11 word_2 : str
12 比較元ビット列
13
14 Returns
15 -------
16 index : int
17 何ビット目まで一致していたか
18 """
19 l = len(word_b1)
20 k = 0
21 for i in range(l):
22 if len(word_b2) <= i or word_b1[i] != word_b2[i]:
23 break
24 k = k + 1
25
26 return k
27
28 def __search_longest_match(self, word_b, node_index=0):
29 """
30 Patriciaを巡回して最長一致を求める
31
32 Parameters
33 ----------
34 word_b : str
35 検索したいビット列
36
37 node_index : int
38 検索開始位置のindex
39
40 Returns
41 -------
42 node_index : int
43 一致した最後のnodeのインデックス
44
45 rest_str : str
46 残りbit列
47
48 match_str : str
49 最後のnodeと一致したbit列
50 """
51
52 sub_str = self.nodes[node_index].sub_str
53
54 match_num = self.__match(word_b, sub_str)
55 if match_num == len(word_b):
56 return node_index, "", word_b
57
58 rest_str = word_b[match_num:]
59 match_str = word_b[:match_num]
60 # ここまでで現在のノードに対するmatch_str、rest_strが求まる
61
62 next_node = self.nodes[node_index].children[int(rest_str[0])]
63 if next_node == -1:
64 return node_index, rest_str, match_str
65
66 return self.__search_longest_match(rest_str, next_node)コード解説
__search_longest_match() メソッドのコードを少し解説します。
__search_longest_match() は、一度呼び出されるごとにノードを1つ巡り、再帰的に呼び出されることで最後のノードまで巡ります。
まず、match_str = word_b[:match_num] までで、現在着目しているノードが対応するアルファベット列(sub_str )に対して、match_str とrest_str を求めます。
（match_str とrest_str は、先程説明したとおり、検索文字列がsub_str に対して一致した部分と、一致しなかった部分を表します。）
このとき、match_str が検索文字列であるword_b と完全に一致した場合、そのノードで丁度探索が終了したことになるので、その時点のnode_index 、rest_str 、match_str を返します。
続いて、現在のノードの情報と、残りの検索文字列を用いて、次のノードへの遷移を行います。
このとき、次のノードが存在しなかった場合は、パトリシア木の末端まで探索し終わったことになるので、この時点で return します。
遷移に成功した場合は、__search_longest_match() を再帰的に呼び出します。
パトリシア木実装(挿入部分)
パトリシア木に単語を挿入するためのinsert() メソッドを実装していきます。
パトリシア木における挿入処理は、分岐のないノードを省略するために、やや複雑な処理を必要とします。
パトリシア木の挿入処理は、大きく2パターンに分けられます。
- 1つ目は、挿入の際に既存のノードの変更が必要なもの。
- 2つ目は、既存のノードの変更が必要ないものです。
図を用いて説明していきます。
パターン１
上の図は、単語「a」, 「b」, 「abc」が格納されているパトリシア木に「ab」というノードを追加するものです。
この場合は、既存のノードの変更が必要な場合になります。
この場合、新たな「ab」のノードは、「a」のノードと「abc」のノードの間に挿入されることになります。
「ab」のノードを「a」のノードの下に挿入したとき、「a」のノードの遷移先は「abc」のノードから変更されることになります。
また、「ab」のノードの下につく「abc」のノードについても、sub_str を変更する必要があります。
一方、既存のノードに変更が必要ない場合もあります。
パターン２
上の図は、先程のパトリシア木に「ba」という単語を追加するものです。
この場合、以下の図のように、既存ノードを変更する必要なく挿入することができます。
このようにパトリシア木では、単語を挿入する際に、ただノードを追加するだけでなく、既存のノードを変更する必要が生じる場合もあります。
コード
これを踏まえて、insert()メソッドのコードを見ていきましょう。
1class Patricia:
2 """
3 Patricia木を表すクラス
4
5 Attributes
6 ----------
7 nodes : PatriciaNode
8 ノードのリスト
9 """
10
11 def insert(self, word, item):
12 """
13 Patriciaに新しい単語を登録する
14
15 Parameters
16 ----------
17 word : str
18 登録する単語
19
20 item : str
21 wordに対応する読み方
22 """
23
24 word_b = self.__word_2_bit(word)
25 node_index, rest_str, match_str = self.__search_longest_match(word_b)
26 node_rest_str = self.nodes[node_index].sub_str[len(match_str):]
27 # node_index : 最後のノードのindex
28 # node_rest_str : ノードの文字列の挿入文字列と一致しなかった部分
29 # rest_str : 挿入文字列のノードの文字列と一致しなかった部分
30 # match_str : 挿入文字列のノードの文字列と一致した部分
31
32
33 if node_rest_str != '':
34 # 新しいノードを付け加える
35 new_node_index = self.__add_node()
36 self.nodes[new_node_index].item = self.nodes[node_index].item
37 self.nodes[new_node_index].children = list(self.nodes[node_index].children)
38 self.nodes[new_node_index].sub_str = node_rest_str
39
40 # 既存のノードを変更する
41 self.nodes[node_index].item = None
42 self.nodes[node_index].children[int(node_rest_str[0])] = new_node_index
43 self.nodes[node_index].sub_str = match_str
44
45
46 if rest_str != '':
47 # 新しいノードを付け加える
48 new_node_index = self.__add_node()
49 self.nodes[new_node_index].item = item
50 self.nodes[new_node_index].sub_str = rest_str
51
52 self.nodes[node_index].children[int(rest_str[0])] = new_node_indexコード解説
まずは、node_index 、node_rest_str 、rest_str 、match_str を求めます。
それぞれの変数の意味は、コメントに書いてあるとおりです。
次に、条件分岐からノードを追加していきます。
条件に当てはまる場合は、ノードを追加するだけでなく既存のノードの変更を必要とします。
条件に当てはまる場合（rest_strがある場合）は、さらに新しいノードを付け加える必要があります。
パトリシア木の実装(検索部分)
続いて、検索部分の実装を行っていきます。
とはいえ、__search_longest_match() の実装が終わっているので、ここは簡単です。
コード
こちらがコードとなります。
1 def query(self, word):
2 """
3 Patriciaを検索する
4
5 Parameters
6 ----------
7 word : str
8 検索したい単語
9
10 Returns
11 -------
12 item : str or None
13 検索結果
14 見つからなかった場合はNone
15 """
16
17 word_b = self.__word_2_bit(word)
18 node_index, rest_str, match_str = self.__search_longest_match(word_b)
19 node_str = self.nodes[node_index].sub_str
20 if match_str == node_str and rest_str == "":
21 return self.nodes[node_index].item
22 return Noneコード解説
__search_longest_match() を実行し、node_index 、rest_str 、match_str と、node_rest_str を取得しています。
検索単語が存在する場合というのは、条件にあるように、node_rest_str とrest_str が空のとき、つまり、ノードの文字列と検索文字列が完全に一致したときです。
よって、このときのみ対応する item を return し、それ以外の場合は単語が存在しないので None を return します。
パトリシア木の実装(全体)
ここまでで、パトリシア木を用いた辞書の実装が終わりました。
すべてのコードをまとめたものが以下になります。
コード
1import sys
2
3VOCAB_SIZE = 2 # アルファベット数
4
5
6class PatriciaNode:
7 """
8 Patricia木の1ノードを表すクラス
9
10 Attributes
11 ----------
12 item : str
13 登録された単語の読み方
14 単語終端ノード以外の場合はNone
15
16 children : list
17 子ノードのリスト
18
19 sub_str : str
20 そのノードに対応する部分文字列
21
22 """
23
24 def __init__(self, item = None, sub_str = ""):
25 self.item = item
26 self.children = [-1 for i in range(VOCAB_SIZE)]
27 self.sub_str = sub_str
28
29
30class Patricia:
31 """
32 Patricia木を表すクラス
33
34 Attributes
35 ----------
36 nodes : PatriciaNode
37 ノードのリスト
38 """
39
40 def __init__(self):
41 root = PatriciaNode()
42 self.nodes = [root]
43
44 def __add_node(self, node=None):
45 """
46 nodesにノードを追加する
47 追加したノードのインデックスを返す
48
49 Parameters
50 ----------
51 node : TrieNode
52 追加するノード
53
54 Returns
55 -------
56 index : int
57 追加したノードのインデックス
58 """
59 if node is None:
60 node = PatriciaNode()
61 self.nodes.append(node)
62 return len(self.nodes) - 1
63
64 def __word_2_bit(self, word):
65 """
66 文字列をビット列に変換する
67 """
68 word_b = ""
69 for c in word:
70 word_b = word_b + format((ord(c) - ord('a')), '08b')
71
72 return word_b
73
74 def __match(self, word_b1, word_b2):
75 """
76 word_1がword_2に先頭から何文字目まで一致しているかを調べる
77
78 Parameters
79 ----------
80 word_1 : str
81 比較対象ビット列
82
83 word_2 : str
84 比較元ビット列
85
86 Returns
87 -------
88 index : int
89 何ビット目まで一致していたか
90 """
91 l = len(word_b1)
92 k = 0
93 for i in range(l):
94 if len(word_b2) <= i or word_b1[i] != word_b2[i]:
95 break
96 k = k + 1
97
98 return k
99
100 def __search_longest_match(self, word_b, node_index=0):
101 """
102 Patriciaを巡回して最長一致を求める
103
104 Parameters
105 ----------
106 word_b : str
107 検索したいビット列
108
109 node_index : int
110 検索開始位置のindex
111
112 Returns
113 -------
114 node_index : int
115 一致した最後のnodeのインデックス
116
117 rest_str : str
118 残りbit列
119
120 match_str : str
121 最後のnodeと一致したbit列
122 """
123
124 sub_str = self.nodes[node_index].sub_str
125
126 match_num = self.__match(word_b, sub_str)
127 if match_num == len(word_b):
128 return node_index, "", word_b
129
130 rest_str = word_b[match_num:]
131 match_str = word_b[:match_num]
132 # ここまでで現在のノードに対するmatch_str、rest_strが求まる
133
134 next_node = self.nodes[node_index].children[int(rest_str[0])]
135 if next_node == -1:
136 return node_index, rest_str, match_str
137
138 return self.__search_longest_match(rest_str, next_node)
139
140 def insert(self, word, item):
141 """
142 Patriciaに新しい単語を登録する
143
144 Parameters
145 ----------
146 word : str
147 登録する単語
148
149 item : str
150 wordに対応する読み方
151 """
152
153 word_b = self.__word_2_bit(word)
154 node_index, rest_str, match_str = self.__search_longest_match(word_b)
155 node_rest_str = self.nodes[node_index].sub_str[len(match_str):]
156 # node_index : 最後のノードのindex
157 # node_rest_str : ノードの文字列の挿入文字列と一致しなかった部分
158 # rest_str : 挿入文字列のノードの文字列と一致しなかった部分
159 # match_str : 挿入文字列のノードの文字列と一致した部分
160
161
162 if node_rest_str != '':
163 # 新しいノードを付け加える
164 new_node_index = self.__add_node()
165 self.nodes[new_node_index].item = self.nodes[node_index].item
166 self.nodes[new_node_index].children = list(self.nodes[node_index].children)
167 self.nodes[new_node_index].sub_str = node_rest_str
168
169 # 既存のノードを変更する
170 self.nodes[node_index].item = None
171 self.nodes[node_index].children[int(node_rest_str[0])] = new_node_index
172 self.nodes[node_index].sub_str = match_str
173
174
175 if rest_str != '':
176 # 新しいノードを付け加える
177 new_node_index = self.__add_node()
178 self.nodes[new_node_index].item = item
179 self.nodes[new_node_index].sub_str = rest_str
180
181 self.nodes[node_index].children[int(rest_str[0])] = new_node_index
182
183 def query(self, word):
184 """
185 Patriciaを検索する
186
187 Parameters
188 ----------
189 word : str
190 検索したい単語
191
192 Returns
193 -------
194 item : str or None
195 検索結果
196 見つからなかった場合はNone
197 """
198
199 word_b = self.__word_2_bit(word)
200 node_index, rest_str, match_str = self.__search_longest_match(word_b)
201 node_rest_str = self.nodes[node_index].sub_str[len(match_str):]
202 if node_rest_str == "" and rest_str == "":
203 return self.nodes[node_index].item
204 return None最後に、Patriciaクラスを利用して単語の登録、検索を行います。
1patricia = Patricia()
2patricia.insert("a", "エー")
3patricia.insert("ab", "エービー")
4patricia.insert("abc", "エービーシー")
5patricia.insert("b", "ビー")
6patricia.insert("bc", "ビーシー")
7patricia.insert("c", "シー")
8
9print(patricia.query("a"))
10print(patricia.query("abc"))
11print(patricia.query("bc"))
12print(patricia.query("abcd"))これを実行すると、以下のような結果になります。
エー
エービーシー
ビーシー
None
辞書にinsert した単語は、きちんと読み方が表示され、そうでない単語はNone となっていることが分かります。
まとめ
お疲れ様でした！
パトリシア木は、トライ木に比べるとやや複雑で理解しにくかったかもしれません。
しかし、一度理解し使えるようになれば、高速でサイズの小さい使い勝手の良いデータ構造です。
トライ木がわかっていればそこまで難しくないと思うので、ぜひチャレンジしてみてください。
こちらの記事もオススメ！
関連記事
2019.08.08トライ木で高速な辞書を作ってみた！トライ木で高速な辞書を作りたい！トライ木（英: trie）というデータ構造を知ってますか？トライ木はテキストを扱う際に...
2020.01.15トリプルアレイで軽量で高速な辞書を作ってみた！軽量で高速に検索できる辞書システムをつくるトリプルアレイというデータ構造をご存知でしょうか？「ダブルアレイ」は聞いたこ...
2020.01.28ダブルアレイで高速でコンパクトな辞書を実装してみた！ダブルアレイを使って辞書を実装してみるダブルアレイは、トライ木を表現することができるデータ構造で、コンパクトで高速に辞...
ライトコードでは、エンジニアを積極採用中！
ライトコードでは、エンジニアを積極採用しています！社長と一杯しながらお話しする機会もご用意しております。そのほかカジュアル面談等もございますので、くわしくは採用情報をご確認ください。
採用情報へ
「好きを仕事にするエンジニア集団」の（株）ライトコードです！ ライトコードは、福岡、東京、大阪、名古屋の４拠点で事業展開するIT企業です。 現在は、国内を代表する大手IT企業を取引先にもち、ITシステムの受託事業が中心。 いずれも直取引で、月間PV数1億を超えるWebサービスのシステム開発・運営、インフラの構築・運用に携わっています。 システム開発依頼・お見積もり大歓迎！ また、現在「WEBエンジニア」「モバイルエンジニア」「営業」「WEBデザイナー」を積極採用中です！ インターンや新卒採用も行っております。 以下よりご応募をお待ちしております！ https://rightcode.co.jp/recruit
